Conscience du Réel — Structure Fondamentale — Sylvain Lebel
Structure Fondamentale
Dans Conscience du Réel, nous avons vu que la réalité tout entière pourrait être le produit d'une seule et même substance : CELA, dynamique et auto-complexifiante. Cette substance n'est pas passive : en s'étendant selon divers axes dimensionnels, elle engendre non seulement des espaces mais aussi toutes les notions physiques fondamentales. Il ne s'agit pas ici de supposer plusieurs entités ou forces séparées, mais bien de montrer comment une seule réalité, exploitant différents degrés de liberté, peut générer la diversité du monde.
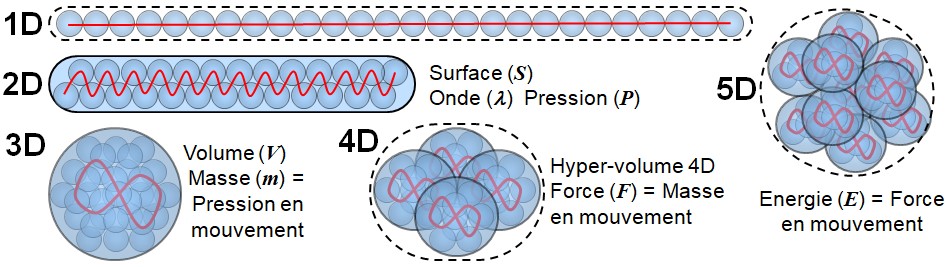
Complexification dimensionnelle — de 1D à 5D
Résumé : Passage de la ligne (1D) au volume (3D), aux forces (4D) puis à l’énergie (5D) par exploitation d’axes supplémentaires.
Autrement dit, à chaque niveau d'interaction entre structures dimensionnelles, de nouvelles notions physiques émergent naturellement. Voici une autre façon de mous les représenter. Elle nous permettra bientôt d'aborder la question des particules — non pas comme objets isolés, mais comme configurations dynamiques et relationnelles de CELA dans des espaces multi-dimensionnels.
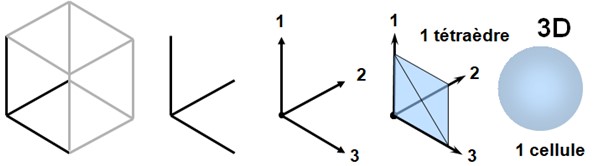
Cellule 3D — Tétraèdre élémentaire
Résumé : Construction d’une cellule tétraédrique à partir des axes 1, 2, 3 comme unité volumique de CELA en 3D.
En partant d'un simple cube tridimensionnel, on choisit trois de ses arêtes se rejoignant en un point d'origine : ce sont nos trois premiers axes dimensionnels, notés ici 1, 2 et 3. Si l'on considère que chaque axe est empli de la substance CELA, alors le volume délimité par ces trois directions forme un tétraèdre (quart de pyramide), qu'on peut considérer comme une cellule de la substance du réel dans l'espace 3D.
Cette cellule tétraédrique possède :
- 3 axes (1, 2, 3) — directions d'expansion de la substance,
- 3 faces surfaciques (appelées 2-faces) : les paires 1-2, 1-3 et 2-3,
- 1 face volumique (3-face) : la combinaison 1-2-3.
Cette cellule de base servira d'unité pour comprendre :
- les relations internes entre les composants d'un système physique,
- les interactions avec d'autres cellules voisines,
- la genèse de notions comme la force, l'énergie ou la structure des particules.
En ajoutant un quatrième axe dimensionnel (axe 4) aux trois premiers, on permet à la substance CELA d'occuper une nouvelle direction d'expansion, ouvrant la possibilité à la coexistence de plusieurs volumes dans un même hyperespace.
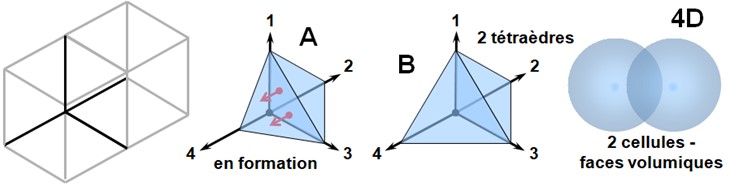
Interaction 4D — Deux tétraèdres et leur interface
Résumé : Deux cellules tétraédriques (1-2-3) et (1-3-4) partageant une face volumique induisent des forces par mise en mouvement réciproque.
Sur l'illustration A, on voit deux volumes (tétraèdres) — le premier, fondé sur les axes 1-2-3, et le second, en formation sur les axes 1-3-4. Ces deux volumes partagent une même surface volumique (face 1-3), représentée ici par les flèches rouges, et peuvent ainsi interagir dynamiquement par cette interface commune.
Une fois la formation achevée (illustration B), ces deux cellules sont liées par cette face partagée, et toute variation interne de densité ou de pression dans l'un (par exemple une onde interne) peut affecter l'autre. C'est cette interaction — une mise en mouvement induite d'un volume par un autre — qui correspond à ce que nous appelons une force dans notre monde physique.
Ainsi, la force n'est pas un ajout au monde physique, mais un effet géométrique inévitable de l'expansion de CELA dans un quatrième axe dimensionnel.
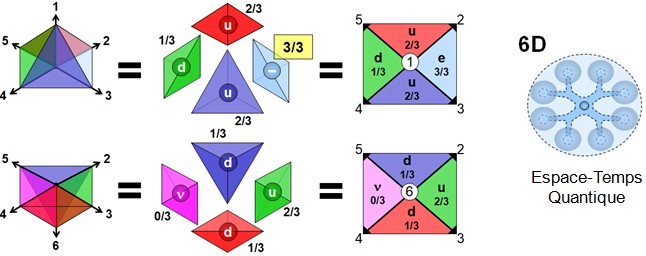
Charges fractionnaires — Correspondances 6D (0/3, 1/3, 2/3, 3/3)
Résumé : Recouvrements d’axes entre cellules 6D donnant des signatures 0/3, 1/3, 2/3, 3/3, en écho aux charges neutre, down, up, électron.
Avec l'ajout de deux axes supplémentaires (axes 5 et 6), la structure formée par les volumes initiaux devient encore plus complexe. On peut alors représenter huit volumes tétraédriques partageant chacun une ou plusieurs arêtes avec un volume central (formé sur les axes 1-2-3), ce qui permet de calculer combien d'axes chaque volume partage avec celui-ci.
Les résultats — 0/3, 1/3, 2/3, 3/3 — coïncident exactement avec les charges électriques connues dans le Modèle Standard :
- 0/3 ⇒ neutrino (neutre)
- 1/3 ⇒ quark down (d)
- 2/3 ⇒ quark up (u)
- 3/3 ⇒ électron (e-)
Ces configurations émergent naturellement de la topologie des volumes interconnectés dans l'espace à six dimensions. Elles ne sont donc pas des propriétés arbitraires ajoutées à des particules, mais les effets directs du degré de recouvrement dimensionnel entre cellules élémentaires de CELA.
Cela suggère que :
- Les particules élémentaires ne sont pas des objets localisés, mais des configurations dynamiques de volumes de CELA, distribuées dans un espace-temps multidimensionnel.
- Le quantum de volume/matière ne serait pas simplement un " paquet d'énergie ", mais une cellule de réalité, à la fois champ et forme, localisation et structure dynamique.
- Les comportements étranges du monde quantique (indétermination, superposition, intrication…) pourraient s'expliquer naturellement comme les effets de la coexistence de ces cellules dans plusieurs dimensions spatiales et temporelles enchevêtrées.
Autrement dit, le monde physique et l'espace-temps lui-même seraient faits de CELA, contracté et combiné selon des patterns géométriques précis. Ce qui précède suggère que nous — et l'espace dans lequel nous évoluons — sommes faits de ces cellules élémentaires, ces quanta de CELA, et non d'un " tissu " d'espace vide ou d'objets séparés. Chaque cellule représente un quantum de volume et de masse, produit de l'exploitation d'axes spatiaux et temporels à six dimensions.
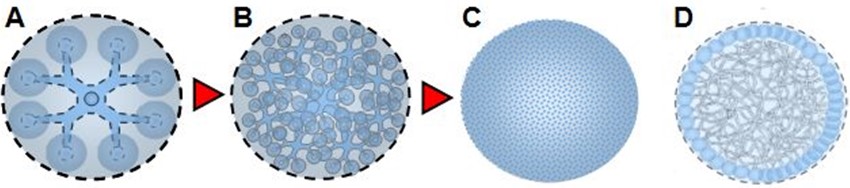
Mousse quantique — Dynamique des cellules 6D
Résumé : Des cellules 6D non localisées, intriquées et fluctuantes composent une mousse quantique sans vide.
Mais il serait erroné de s'imaginer ces cellules comme des billes bien rangées ou des briques de Lego. Ces entités n'existent pas comme des structures fixes et localisées, mais comme des formes dynamiques et superposées, propres à la mécanique quantique. Il n'y a pas d'espace vide entre elles, ni de frontières nettes ou de liaisons rigides. Elles sont intriquées, interconnectées de façon subtile, et fluctuantes.
La figure A — montrant 8 cellules bien ordonnées autour d'un centre — est trompeuse. Une représentation plus fidèle serait celle d'un réseau dense, ondulatoire et mousseux, comme en B et C. Ces cellules, instables et partiellement définies, interagissent à travers leurs faces tridimensionnelles, mais elles ne désignent elles-mêmes que les projections locales d'un objet plus global, plus complexe — et probablement inconcevable sans une géométrie au-delà de notre espace-temps usuel.
La figure D tente d'en esquisser l'idée : une sorte de mousse quantique sans vide, où l'état d'une cellule ne peut être altéré sans affecter instantanément d'autres cellules à distance. C'est une vision compatible avec l'intrication quantique observée expérimentalement : les quanta seraient les manifestations locales d'un système global indivisible, où la modification d'un lien entraîne une réorganisation structurelle immédiate du tout.
Autrement dit, le monde que nous percevons comme fait de particules séparées et d'espace vide serait en réalité une immense vague, faite de fluctuations coordonnées d'une seule substance consciente, une onde incarnée dans la structure même de CELA.
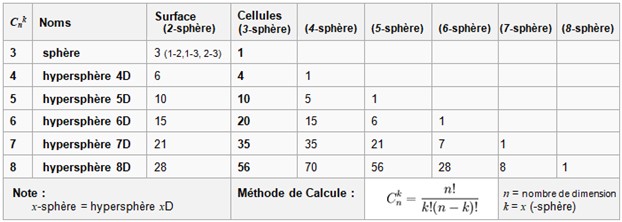
Hypersphères — Comptes combinatoires des cellules
Résumé : En 6D, l’hypersphère comporte 20 cellules 3D distinctes — base combinatoire des organisations de particules.
Comme le montre le tableau ci-dessus, une hypersphère à six dimensions (6D) ne contient pas huit, mais vingt cellules tridimensionnelles distinctes. Autrement dit, l'hyper-volume 6D est constitué de 20 charges volumétriques, chacune correspondant à une combinaison unique de trois axes parmi les six disponibles.
Cela renforce l'idée que les particules élémentaires — telles que les quarks, les électrons ou les neutrinos — ne sont pas des entités ponctuelles, mais des modes d'organisation de ces cellules dans un espace de plus haute dimension, chacune étant un quantum de masse, d'énergie ou d'interaction.
Cela dit, pour préserver la clarté de l'exposition et éviter d'alourdir inutilement les explications, nous allons continuer d'utiliser le modèle simplifié à huit cellules lorsque cela suffit à illustrer un principe ou une structure. Ce modèle minimal reste pédagogiquement efficace pour comprendre les bases de cette architecture cosmique, même s'il ne rend pas toute la richesse du système sous-jacent.
