Conscience du Réel — Matière — Sylvain Lebel
Matière
Si l'espace-temps se déploie dans un hyper-volume à six dimensions, il semble que ce ne soit pas la limite de l'extension de CELA. Lorsqu'une pression interne devient trop élevée, dépassant la capacité des spations à la contenir dans les six axes, une rupture de confinement pourrait survenir.
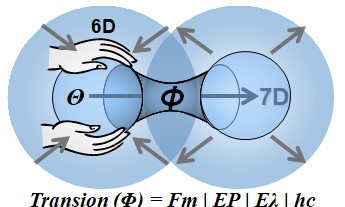
Transion 6D → 7D
Résumé : Sous pression extrême, une portion de CELA migre sur un 7e axe dimensionnel, ouvrant un nouveau domaine cosmique.
Dans ce cas, une portion de la substance serait contrainte à migrer sur un septième axe dimensionnel, s'ouvrant alors un nouveau domaine cosmique. Ce processus peut être compris comme une transtension : une tension spatiale si extrême qu'elle provoque un transfert de substance vers un niveau d'organisation supérieur. Le spation s'y « vide » partiellement, et son contenu énergétique prend forme dans un nouvel espace (7D), plus rare, plus condensé.
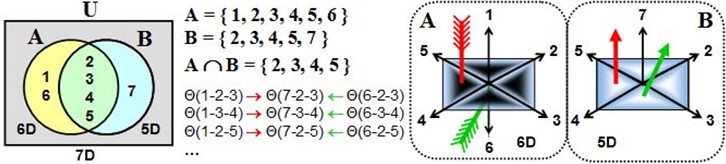
Intersection 6D/5D en 7D
Résumé : Schéma simplifié d’interfaces 6D/5D en 7D ; phénomènes détaillés focalisés sur la zone A.
Cette représentation est un modèle simplifié car la présence d'un septième peut impliquer la formation de 15 nouvelles charges de spations dans le domaine B. Nous y reviendrons. Pour l'instant nous nous limiterons aux phénomènes se déroulant en A.
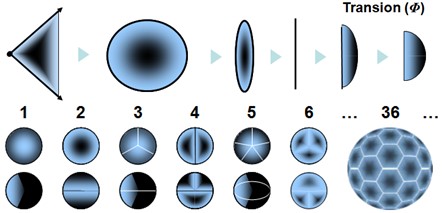
Typologie des transions
Résumé : Familles de transions suivant le nombre de spations transférés simultanément (1 à 36).
Compte tenu de l'énorme pression régnant dans l'espace-temps, la disparition de spations pourrait permettre aux spations de même charge tridimensionnelle qui les entours d'y être poussés, comprimés et transférés à leur tour et à la chaîne, un peu comme si on avait créé un trou permettant aux spations de cette charge de s'écouler vers un second domaine cosmique. Nous désignons sous le nom de transion ce point dans l'espace-temps où se transfèrent les spations et représentons-les comme ci-haut.
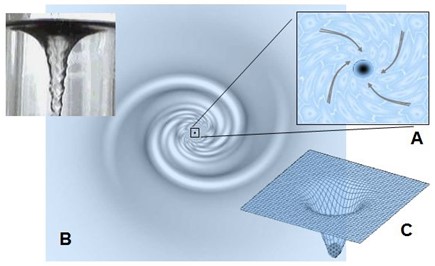
Vortex quantique engendré par un transion
Résumé : Le transion active un écoulement rotatif convertissant la pression en énergie cinétique ; stabilité par viscosité dynamique.
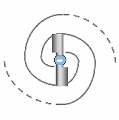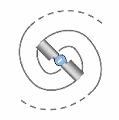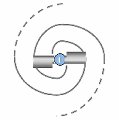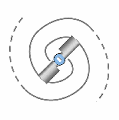
Un transion actif dans l'espace-temps ne se contente pas de transférer des spations : il engendre un champ d'écoulement. Cette dynamique convertit l'énergie de pression colossale de l'espace-temps en énergie de mouvement, donnant ainsi naissance à un phénomène auto-organisé, stable et croissant : le vortex.
Comme illustré en (A), les spations environnants s'organisent en rotation autour du point d'écoulement, créant un vortex quantique qui canalise et régule le flux de substance. Ce comportement n'est pas arbitraire : il est rendu possible par la viscosité dynamique du milieu — rappelons que les spations peuvent glisser les uns sur les autres, mais en s'entraînant mutuellement, générant des forces de rappel.
La figure (B) donne une analogie classique : celle d'un vortex dans un liquide, capturant visuellement la dynamique de chute structurée. Mais contrairement à un liquide, ce flux ne tombe pas vers le bas ; il migre dans une nouvelle direction dimensionnelle.
En (C), on voit que la pression locale diminue vers le cœur du vortex, comme si l'espace se creusait. L'énergie de pression y est progressivement transformée en énergie cinétique. Ce gradient rend le phénomène auto-alimenté : plus l'écoulement s'intensifie, plus il vide l'espace-temps local de sa pression, et plus il attire de substance.
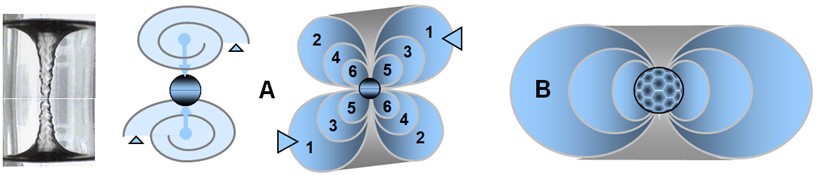
Configurations de transion
Résumé : Deux vortex contrarotatifs (petit nombre pair de spations) vs vortex unique (transfert plus important), stabilité accrue pour le second.
Un transion transférant simultanément deux (ou un petit nombre pair) de spations ne génèrerait pas un mais deux vortex, comme le montre la figure (A). Ces vortex seraient inverses et contrarotatifs, faute de quoi la configuration deviendrait instable. Chacun d'eux attire les spations depuis des directions opposées, les comprimant vers un même point de transion où ils disparaissent deux à la fois.
Les deux vortex, montés l'un sur l'autre, prennent ici la forme de coquilles d'escargot latérales. Ils se chargent symétriquement, créant un champ de pression croisé centré sur la disparition des spations concernés.
Cependant, plus le nombre de spations transférés simultanément augmente, plus cette configuration double devient instable et improbable. En revanche, une configuration à vortex unique (figure B) gagne en stabilité, cohésion et efficacité avec le nombre de spations transférés.
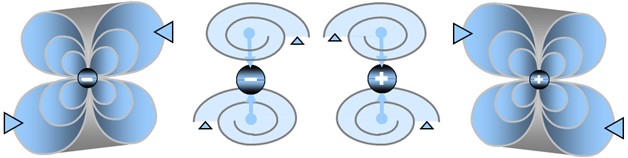
Polarités et vortex de fermions
Résumé : Deux polarités de charge possibles selon le sens d’écoulement des spations à travers les vortex d’une même particule.
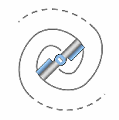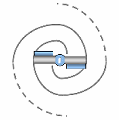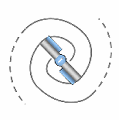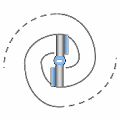
Toute particule de type fermion — c'est-à-dire toute particule dotée de masse gravitationnelle — pourrait se retrouver selon deux polarités au niveau du sens de la charge en spations des vortex. Autrement dit, les spations qui s'écoulent dans les vortex d'une même particule pourraient le faire dans un sens ou dans l'autre, comme on le voit au centre de l'image. Cette polarité donnerait lieu à deux formes opposées d'une même structure.
Tout fermion disposerait d'un moment cinétique intrinsèque, autrement dit d'une masse en rotation. Ce mouvement résulterait à la fois de la rotation des spations dans chaque vortex et de la rotation des vortex eux-mêmes, lesquels peuvent, selon les conditions locales, prendre de l'avance ou du retard sur le flux d'écoulement.
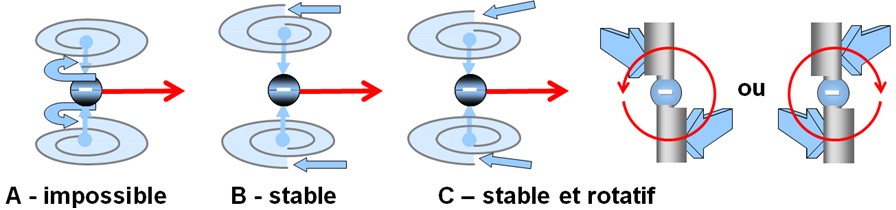
Dynamiques de fermion en translation
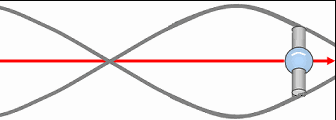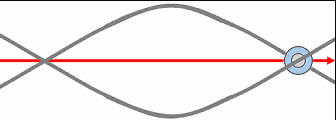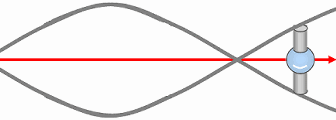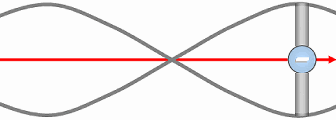
Résumé : États stables (B, C) vs impossible (A) ; rotation globale et onde vectorielle statique de longueur d’onde ∝ 1/vitesse.
Toutefois, lorsque les vortex se mettent en mouvement de translation à travers le champ spatio-temporel, leur rotation propre tend à s'annuler, convertie en rotation globale de la particule. Autrement dit, le spin intrinsèque des vortex devient le moment cinétique orbital du système, ce qui confère à la particule une rotation nette dans l'espace. Cette orientation dépend de l'écoulement relatif du champ spatio-temporel, et de l'avance ou du retard pris par les vortex par rapport à cet écoulement. Deux états stables sont alors possibles, tandis qu'un état où les deux vortex tourneraient en sens opposé (comme en A) serait mécaniquement instable et impossible.
La rotation du fermion (ex: électron) implique l'apparition d'un champ secondaire unique produisant une onde vectoriel et statique dans l'espace-temps dont la longueur serait inversement proportionnelle à sa vitesse (ou énergie cinétique). Ceci car plus la vitesse est grande, plus petits sont les vortex.

Scission d’un double vortex
Résumé : Sous compression, un double vortex pourrait donner deux vortex simples (spin unique, deux polarités, 1–3 spations).
Par contre, toute particule à double vortex soumise à une compression suffisante pourrait peut-être être séparée en deux particules à simple vortex. Dans ce cas, le transion à simple vortex serait vite accéléré à la vitesse de propagation des ondes dans l'espace par compression de son champ sur sa partie arrière. Il pourrait n'avoir qu'un sens de spin, et pourrait se présenter selon deux sens de charge et faire transiter de un à trois spations à la fois.

Trois types de vortex de transion
Résumé : Vortex #1–#3 transitant 1–3 spations ⇒ 2F/4F/6F (masse et instabilité croissantes ; champ plus étendu).
Chaque vortex de transion pourrait faire transiter un, deux ou trois spations simultanément, et ainsi comporter de un à trois couloirs d'intégration. Ce mécanisme implique l'existence de trois formes distinctes de fermions pour chaque charge et chaque polarité de vortex.
Ces variantes, analogues aux trois générations de particules connues en physique (électron, muon, tau ; quarks up / charm / top, etc.), se distingueraient par :
- leur masse croissante, due à l'effet d'inflaréaction : plus il y a de couloirs, plus la différence de vitesse entre eux est faible, ce qui augmente localement la pression et la densité de l'espace-temps environnant ;
- l'étendue de leur champ d'interaction dans le milieu spatiotemporel ;
- leur instabilité croissante : les particules à plusieurs couloirs subissent en translation une asymétrie dans leur écoulement, ce qui les rend plus susceptibles de se désintégrer.
Ainsi, le modèle prévoit que :
- Les particules à un seul couloir seraient les plus légères, stables et fréquentes (comme l'électron ou le quark up),
- Celles à deux couloirs auraient une masse intermédiaire et une stabilité réduite (muon, quark charm...),
- Celles à trois couloirs seraient très massives, instables, et ne se maintiendraient que dans des conditions énergétiques extrêmes (tau, quark top...).
Ce schéma offre une explication géométrique et dynamique à la hiérarchie des masses et à l'instabilité des particules lourdes, sans invoquer des propriétés arbitraires, mais en les déduisant de la structure même des transions et de leur interaction avec le milieu spatiotemporel.
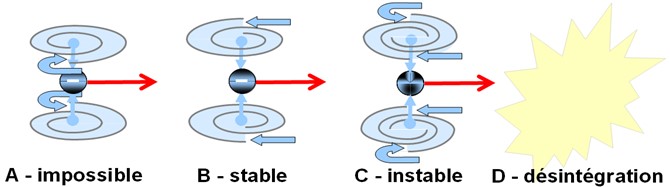
Stabilité et désintégration
Résumé : Synchronisation des vortex ⇒ stabilité ; désynchronisation ⇒ instabilité puis désintégration.
Les spations pourraient donc donner naissance à des particules de leur charge tridimensionnelle. Les interactions entre spations, et les particules qu'ils forment, dépendraient nécessairement du nombre d'axes dimensionnels qu'ils ont en commun, et par rapport à la charge de l'électron (1-2-3), dites charge Q (3/3) :
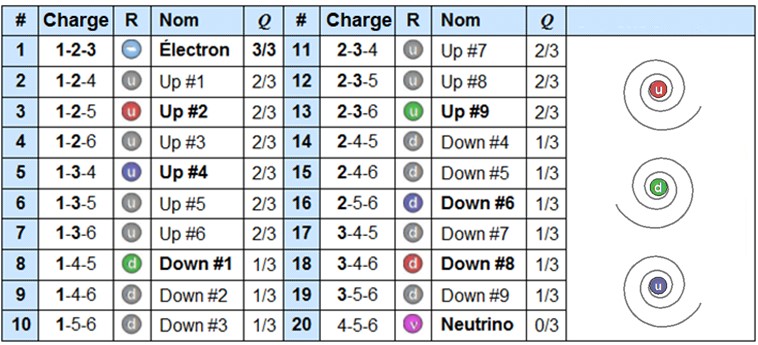
Tableau des 20 particules élémentaires
Résumé : Combinaisons d’axes 6D ⇒ charges {0/3,1/3,2/3,3/3} ; typologie (e, u, d, ν) par recouvrements dimensionnels.