Consciousness of the Real

If space-time unfolds within a six-dimensional hyper-volume, this does not appear to mark the limit of THAT's extension. When internal pressure becomes too great — surpassing the ability of spations to contain it along six axes — a confinement rupture may occur.

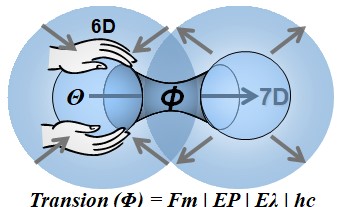
Transion from 6D to 7D: excessive internal pressure forces part of the substance to migrate along a seventh dimensional axis, opening a new cosmic domain.

In such a case, a portion of the substance is compelled to migrate along a seventh dimensional axis, thereby opening a new cosmic domain. This process can be understood as a transtension: a spatial tension so extreme that it causes a transfer of substance to a higher level of organization. The spation is thus partially "emptied," and its energetic content takes form in a new (7D) space, rarer and more condensed.

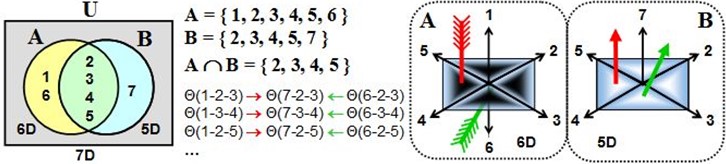
Intersection diagram between two spatial structures, 6D and 5D, within a 7D space, showing spation trajectories across shared dimensions.

This depiction is a simplified model, as the presence of a seventh axis could imply the formation of 15 new spation charges in domain B. We will return to this point later. For now, we will limit ourselves to phenomena occurring within domain A.

Illustration of different types of transions based on the number of spations transferred simultaneously, from 1 to 36, represented by spherical transition structures.

Given the enormous pressure reigning within space-time, the disappearance of spations could allow surrounding spations of the same three-dimensional charge to be pushed, compressed, and transferred in turn, in a chain reaction-much like creating a hole through which spations of that charge can drain into a second cosmic domain. We refer to this point in space-time where spations transfer as a transion, as illustrated above.

Illustration of the quantum vortex generated by an active transion: (A) surrounding spations organize into a rotational flow around the outflow point, forming a stable, self-organized flow field; (B) visual analogy with a liquid vortex; (C) local pressure drop and conversion of pressure energy into kinetic energy in a self-sustained gradient.

An active transion in space-time does not merely transfer spations: it generates a flow field. This dynamic converts the colossal pressure energy of space-time into kinetic energy, thereby giving rise to a self-organized, stable, and growing phenomenon: the vortex.

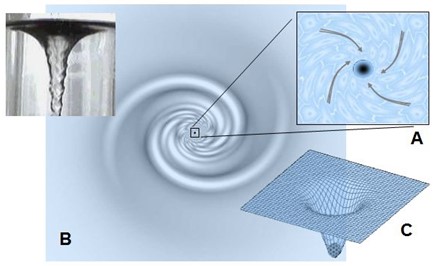
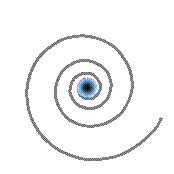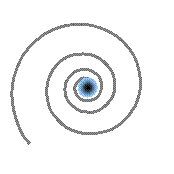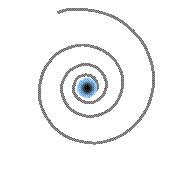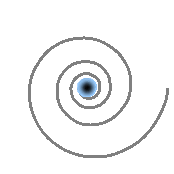
As shown in (A), surrounding spations organize into a rotational motion around the flow point, forming a quantum vortex that channels and regulates the flux of substance. This behavior is not arbitrary: it is made possible by the dynamic viscosity of the medium — recall that spations can slide over one another but entrain each other in the process, generating restorative forces.

(B) offers a familiar analogy: a vortex in a liquid, visually capturing the structured falling motion. However, unlike a liquid, this flux does not fall downward — it migrates into a new dimensional direction.

In (C), we observe that local pressure decreases toward the vortex's core, as though space were being hollowed out. Pressure energy is gradually transformed into kinetic energy. This gradient renders the phenomenon self-sustaining: the more intense the flow, the more local space-time is emptied of its pressure, and the more substance is drawn in.

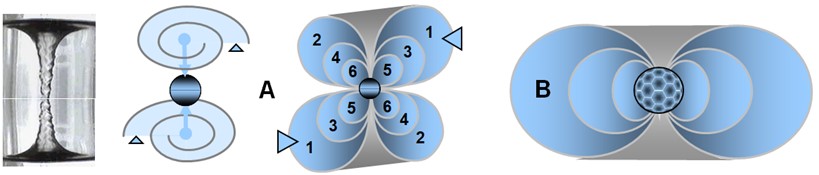
Illustration of two transion configurations: (A) two counter-rotating vortices generated by a transion transferring two spations simultaneously; opposing flows converge toward a shared disappearance point; (B) single-vortex configuration induced by a transion transferring a larger number of spations, producing a stable and coherent pressure field.

A transion transferring two (or a small even number) of spations simultaneously would not generate one but two vortices, as shown in figure (A). These vortices would be inverse and counter-rotating; otherwise, the configuration would become unstable. Each vortex draws in spations from opposite directions, compressing them toward the same transion point where they disappear in pairs.

The two vortices, stacked on top of each other, resemble lateral snail shells. They charge symmetrically, creating a cross-pressure field centered on the disappearance of the corresponding spations.

However, as the number of simultaneously transferred spations increases, this dual configuration becomes increasingly unstable and improbable. In contrast, a single-vortex configuration (figure B) gains in stability, cohesion, and efficiency with the number of spations transferred.

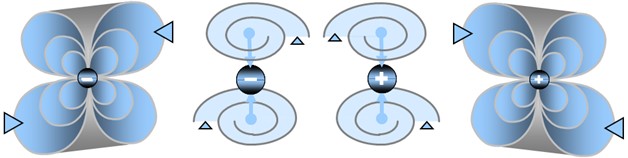
Representation of vortices associated with fermion-type particles, showing two opposite polarities in the direction of spation flow; in the center, opposing charge configurations (- and +) illustrate the two possible flow directions through the vortices of a single particle, resulting in two mirrored forms of the same structure.

Any fermion-type particle — that is, any particle with gravitational mass — could exist in two polarities with respect to the direction of spation charge within its vortices. In other words, the spations flowing through the vortices of a given particle could move in one direction or the other, as seen at the center of the image. This polarity would give rise to two opposite forms of the same structure.

Animation showing the intrinsic angular momentum of a fermion, illustrated by a spiral converging toward a core. This momentum results from both the rotation of spations within the vortex and the rotation of the vortex itself, which may lead or lag the flow depending on local conditions.

Every fermion would possess an intrinsic angular momentum, in other words, a rotating mass. This motion would result both from the rotation of spations within each vortex and from the rotation of the vortices themselves, which may, depending on local conditions, advance or lag behind the flow.

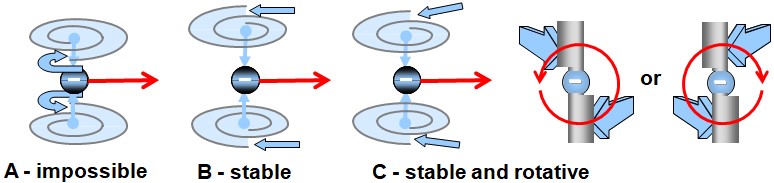
Illustration of the dynamic conditions of a moving fermion: (A) unstable and impossible configuration due to opposing vortex flows; (B) stable configuration with balanced opposing vortices; (C) stable and rotating configuration, where the fermion’s spin generates a secondary vector and static field in spacetime, with a wavelength inversely proportional to its speed (or kinetic energy), since higher speeds correspond to smaller vortices.

However, when the vortices undergo translational motion across the space-time field, their intrinsic spin tends to cancel out, being converted into the orbital angular momentum of the system. That gives the particle a net rotation in space. This orientation depends on the relative flow of the space-time field, and on whether the vortices lead or trail that flow. Two stable states are thus possible, while a state where the two vortices spin in opposite directions (as in A) would be mechanically unstable and impossible.

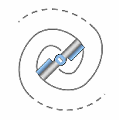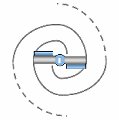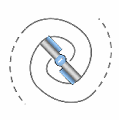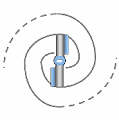
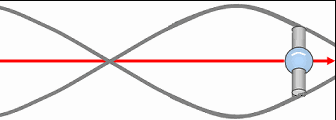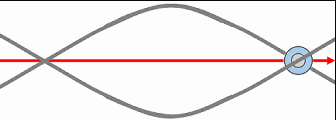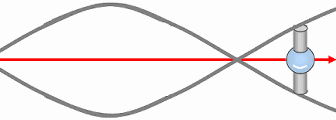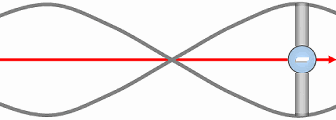
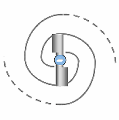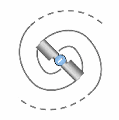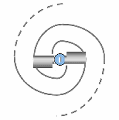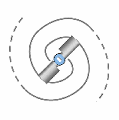
Visualization of a spinning fermion (e.g., electron) generating a static vector wave in spacetime. This secondary wave is centered on the fermion’s rotation axis, and its wavelength decreases as the particle’s speed (or kinetic energy) increases, due to smaller vortices at higher velocities.

The rotation of the fermion (e.g., an electron) implies the emergence of a unique secondary field producing a vectorial and static wave within space-time, whose wavelength would be inversely proportional to its speed (or kinetic energy). This is because, as speed increases, the vortices become smaller.

Diagram showing that a double-vortex particle, under sufficient compression, could split into two single-vortex particles. These elementary particles, quickly accelerated to the speed of wave propagation, would move forward due to rear field compression. They would have a single spin orientation, two possible charge polarities, and could transfer one, two, or three spations at a time.

However, any double-vortex particle subjected to sufficient compression could perhaps be split into two single-vortex particles. In such a case, the single-vortex transion would quickly accelerate to the wave propagation speed in space, driven by compression of its rearward field. It might have only one spin direction and appear in two charge orientations, transferring from one to three spations at a time.

Illustration showing three types of transion vortices (#1 to #3), each transferring one, two, or three spations simultaneously, forming 2F, 4F, and 6F respectively. These vortices correspond to three types of fermions with one, two, or three integration lanes. The zoomed views show the internal spation structure, highlighting the increase in local pressure, mass, and instability as the number of lanes increases.

Each transion vortex could transfer one, two, or three spations simultaneously, and thus comprise one to three integration channels. This mechanism implies the existence of three distinct forms of fermions for each charge and each vortex polarity.

These variants — analogous to the three known generations of particles in physics (electron, muon, tau; up/charm/top quarks, etc.) — would be distinguished by:

Their increasing mass, due to the inflareaction effect: the more channels there are, the smaller the velocity difference between them, which locally increases pressure and space-time density;
The extent of their interaction field in the space-time medium;
Their increasing instability: multi-channel particles experience translational asymmetry in their flow, making them more prone to decay.

Thus, the model predicts that:

Single-channel particles would be the lightest, most stable, and most common (like the electron or up quark);
Two-channel particles would have intermediate mass and reduced stability (muon, charm quark...);
Three-channel particles would be very massive, unstable, and exist only under extreme energetic conditions (tau, top quark...).

This scheme offers a geometric and dynamic explanation for the mass hierarchy and instability of heavy particles, not by invoking arbitrary properties, but by deducing them from the very structure of transions and their interaction with the space-time medium.

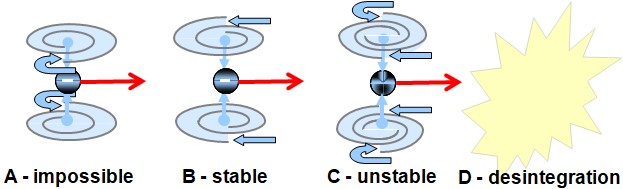
Diagram showing four possible vortex configurations for a moving particle: A – impossible configuration (unstable opposing flows), B – stable configuration with synchronized vortices, C – unstable configuration (increasing vortex desynchronization), D – particle disintegration. This diagram provides a geometric and dynamic explanation for mass hierarchy and particle instability, deriving them from the structure of transions and their interaction with spacetime, without relying on arbitrary properties.

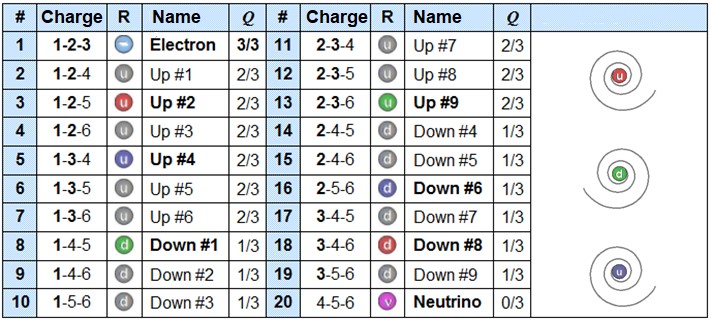
Spations could thus give rise to particles of their corresponding three-dimensional charge. The interactions between spations and the particles they form-would necessarily depend on the number of dimensional axes they share, referenced against the electron's charge (1-2-3), also called Q charge (3/3):

Table showing 20 elementary particles formed from three-dimensional combinations of spations. Each particle is defined by a charge (three dimensional axes), a type (electron, up, down, neutrino), a graphical vortex representation, and a Q value expressing its charge relative to that of the electron (3/3). This model suggests that interactions between spations and the particles they form depend on the number of shared dimensional axes.

Consciousness of the Real — Matter — Sylvain Lebel

Matter