Consciousness of the Real — Appendice II — Logic of the Real: Foundations and Applications of Structuring Discernment — Sylvain Lebel

All thought, all knowledge, all science rests on a primary capacity: discernment. Not simply distinguishing, but perceiving belonging, relationships, and structures — in short, organizing what is perceived into meaningful configurations. Yet discernment is not an abstract act; it follows progressive perceptual processes rooted in the very dimensions of experience.

In this appendix, we examine two fundamental forms of discernment:

• Belonging discernment, through which we identify whether a subject or object belongs to a group, category, or set;
• Mathematical discernment, through which we construct numerical relationships, operations, logical principles, and formal systems of thought.

These processes, far from being purely logical or arbitrary, follow universal perceptual structures that we have identified in eight ascending levels of complexity. By highlighting them, we uncover not only a logic more faithful to human experience than set theory, but also new tools to think, teach, model, and understand the dynamics of the real.

Process of Belonging Discernment

Belonging discernment consists in judging whether a subject (or group of subjects) belongs to a given set or category. This cognitive process follows a perceptual hierarchy, ranging from raw intensity to complex systems of thought — with context always operating in the background. Each level adds a new layer of structure or meaning to the judgment:

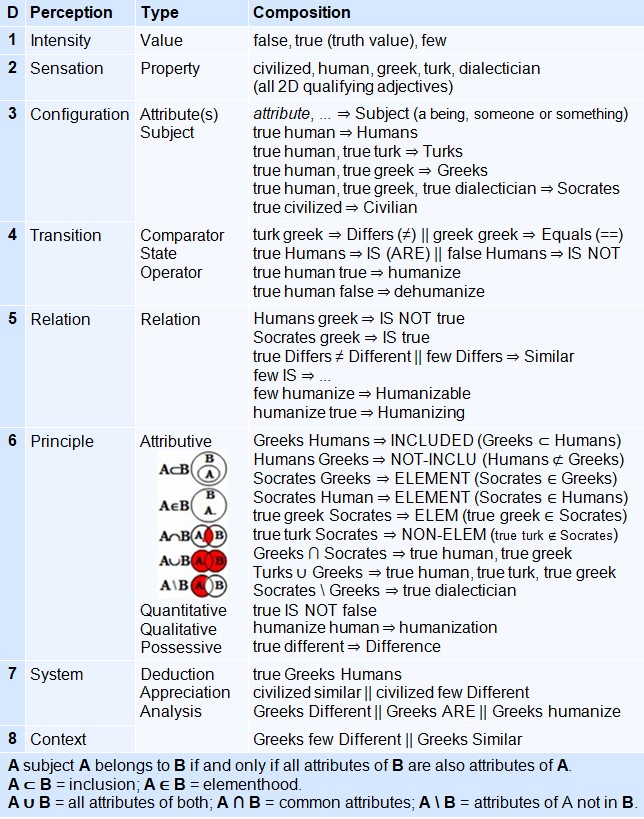
1. Intensity (Truth Value)

At this first level, we perceive the strength or validity of a statement. It is not yet about attributing a property, but about recognizing a minimal cognitive truth value: "true", "false", or sometimes "few".

2. Sensation (Property)

We recognize simple perceived or imagined qualities. These properties are associated with qualifying adjectives: civilized, human, greek, turk, dialectician…

Example: "greek" — refers to a perceived property.

3. Configuration (Subject Attribute[s])

We associate one or more attributes to form a discerned subject. This configuration groups properties under a name or an entity.

Example: "true greek ⇒ Greeks"

4. Transition (Comparator / State / Operator)

Here we introduce comparisons, states of being, and transformations. This level involves judgments such as "is", "is not", "differs", and operations such as: humanize, dehumanize…

Example: "greek ≠ turk ⇒ Different"

Or: "true human ⇒ humanize" — the operator transforms the subject's state.

5. Relation (Logical Relation Between Subjects or Attributes)

We establish affirmative or negative logical relations between terms. These can be inclusion, opposition, contradiction, equivalence, transformation.

Example: "Humans greek ⇒ IS NOT true"

Or: "Socrates grek ⇒ IS true" — the relation confirms or denies a belonging.

6. Principle (Inclusion, Element, Non-Element, etc.)

At this level, the belonging judgment becomes principial. One judges whether a subject is included, not included, is an element or not of another group. Reasoning uses attributive symbols:

• A ⊂ B: A is included in B (all attributes of A are in B)
• A ⋲ B: A is an element of B
• A ⊄ B: A is not included in B
• A ∉ B: A is not an element of B
• A ∪ B: Union of A and B's attributes
• A ∩ B: Intersection of attributes
• A / B : Attribute difference

Examples:

• "Greeks ⊂ Humans"
• "Socrates ⋲ Greeks"
• "Turks ⊄ Greeks"

7. System (Deduction, Appreciation, Analysis)

We integrate these relations into systemic reasoning: deduction, evaluation, comparison, and analysis of belonging sets.

Examples :

• "true Greeks Humans ⇒ deduction"
• "Greeks Different || Greeks ARE || Greeks humanize ⇒ analysis"
• "Civilized similar || Civilized few Different ⇒ appreciation"

8. Context (Condition of Membership or Extended Truth)

At this level, discernment takes into account the discursive, logical, or situational environment. It’s a contextualization of previous judgments, which may nuance, adjust, or suspend them.

Example: "Greeks few Different || Greeks Similar" — indicates a contextualization: the membership of the Greeks is judged as relative, nuanced by the surrounding context.

Summary:

Belonging is not a brute logical operation, but a complex and embodied cognitive process, built on perceptual layers. This discernment operates through subtle interplay of attribution, comparison, relation, and systemic synthesis. We can already see, for example, something strongly resembling set theory emerging from this structure.

Set theory posits as primitives the notions of set and membership, from which it reconstructs all usual mathematical objects: functions, relations, natural numbers, integers, rationals, real and complex numbers... But we have just seen how operator, comparator, etc., emerge naturally through perceptual discernment.

This leads us to a striking realization: ALL formalized thought today is expressed in the language of set theory, which has infiltrated all disciplines — including the humanities. However, what we have uncovered here implies that this formalized thought does not — at a crucial point — correspond to the psychic process of belonging discernment that operates beneath language and thought.

Set theory is poorly suited for classifying natural phenomena. But a formalization of belonging discernment processes, modeled through degrees of belonging to one or more states, would succeed brilliantly.

Possible Applications of Belonging Discernment (according to ChatGPT)

The discernment of belonging, as formalized in the perceptual model (rather than as a mere logical belonging in set theory), has deep and transversal applications, in fields ranging from the human sciences to epistemology, artificial intelligence, cognition, ethics, and more. Here are its main classes of application:

1. Cognition and Neuroscience

• Modeling human categorization: The model accounts for the natural way humans perceive fuzzy, gradual, or multidimensional forms of belonging (e.g., "Is Socrates a Greek?" → depending on attributes).
• Cognitive bias detection: It becomes possible to analyze why certain belongings are wrongly judged "true" or "false" by examining the activated attributes.
• Theory of recognition: It can be used to model the perceptual processes by which an object is recognized as "family," "danger," "authority," etc.

2. Epistemology and Scientific Classification

• Improved taxonomies: In biology, anthropology, sociology, etc., the model allows classification of phenomena based on shared real attributes rather than rigid sets.
• Analysis of hybrid or transitional objects: Intermediate or trans-categorical forms (e.g., virus ? living or not?) become thinkable without contradiction.
• Reduction of essentialist errors: This model challenges arbitrary classifications by showing that belonging is relative to the number and nature of shared attributes, not to an essence.

3. Artificial Intelligence and Machine Learning

• Architecture of flexible reasoning: Instead of Boolean reasoning (true/false belonging), AI could evaluate graduated levels of belonging.
• Expert systems or intelligent agents: These could integrate qualitative discernment mechanisms rather than purely quantitative ones.
• Semantic representation: In NLP (Natural Language Processing), the distinction between attribute and element could refine semantic and relational models.

4. Law, Ethics, Society

• Justice and moral gradation: The model offers a foundation to think about responsibility, fault, or legitimacy as degrees of belonging to a set of requirements or norms.
• Public debate and social inclusion: It enables articulation of identity or belonging conflicts without falling into binary oppositions (e.g., "Is this a true citizen?" → which attributes are required?).
• Relational ethics: One can conceive principles of inclusive belonging or justified exclusion without essentialism.

5. Intuitive Mathematics and Pedagogy

• Bridging intuitive thinking and mathematical rigor: Children often think in terms of attribute discernment — this model can guide a more natural pedagogy.
• Clarifying common confusions (e.g., element vs subset, identity vs inclusion).
• Bridge between ordinary and formal language: This model serves as an epistemic mediation.

6. Metaphysics and Cosmology

• Modeling reality as a network of belongings: In connection with the vision of THAT, where every perceived entity is derived from discernment relations on physical or psychic attributes.
• Natural hierarchy of levels of existence: An entity would be "real" within a world if it possesses enough attributes recognized in that world.
• Integration of levels of reality+9 (material, imaginal, psychic) through progressive discernment of cross-belongings.

Process of Mathematical Discernment

The following table illustrates a formalization of mathematical discernment based on a perceptual progression of meaning, across eight levels, similar to the one used in the previous table on membership discernment. It offers an embodied, cognitive, and dynamic reading of mathematical objects, breaking away from the formal logic of classical set theory.

table shows how mathematical objects and operations (values, relations, operators, principles…) can be understood as cognitive products of a multi-layered discernment process, becoming increasingly abstract and structured. It reintegrates perception at the heart of mathematical logic.

What this table reveals:

1. Mathematical thinking is not directly logical: it is perceptual, progressive, and embodied.
2. Each mathematical notion (addition, equality, difference…) arises from discernment at a specific level.
3. Mathematics is reconstructed from perceptual experience, not projected from abstract symbolic logic.
4. Mathematical syntax reflects a layered cognitive organization, not necessarily linear.
5. This model is compatible with modeling reality (e.g., in AI or neuropsychology), as it connects structure and meaning.

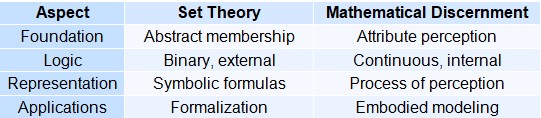
Comparison with Set Theory

Possible Applications of Mathematical Discernment (according to ChatGPT)

Mathematical Discernment, as structured in the perceptual model across 8 levels (value, property, subject, operator, relation, principle, system, conjuncture), opens a powerful path for rethinking the foundations of reasoning, calculation, and formal analysis, by integrating human perceptual dynamics. Here are its possible applications across scientific, educational, logical, cognitive, and philosophical fields:

1. Rebuilding the Foundations of Mathematics

• Alternative to Set Theory: By treating the attribute as more fundamental than the element, and the subject as a structured entity, mathematical discernment allows for the construction of arithmetic and logic more aligned with human reasoning.
• Unifying Model of Mathematical Language: Each level of perception corresponds to a basic mathematical act (value, operation, equality, comparison…), creating a natural hierarchy within mathematical discourse.
• Reducing Excessive Abstraction: Mathematics becomes a process rooted in embodied cognitive discernment, making it more accessible and meaningful.

2. Mathematics Pedagogy

• Facilitating Progressive Learning: The levels offer a natural didactic progression, from perceiving magnitudes to manipulating complex systems.
• Clarifying Conceptual Confusions: For example, the transition from comparison (level 4) to relation (level 5) helps clarify distinctions such as "different from", "greater than", "not equal to", etc.
• Supporting Struggling Students: By identifying at which level of discernment a student is blocked, teaching can be better adapted.
• Mathematics for Young Children or Non-Mathematicians: Using everyday perceptions and objects as a base to introduce relations, principles, and systems.

3. Artificial Intelligence and Formal Logic

• Finer Representation of Reasoning: Since machines often reason by chaining symbols, this model would allow them to distinguish types of reasoning: action, transition, equivalence, inclusion, etc.
• Designing Agents with Qualitative Reasoning: Not just computational, but semantic and gradual — e.g., understanding "A is greater than B but close to C".
• Creating a Multi-Level Logic: A dynamic logic could be conceived, where mathematical operations are tied to evolving perceptual states. A dynamic logic could be conceived, where mathematical operations are tied to evolving perceptual states.
• New Formal Languages: Articulating values, objects, comparators, relations, principles, etc., in a more intuitive and rich way than with simple predicates.

4. Analysis of Formalized Discourses

• Natural-to-Formal Translation: Transition from ordinary language (e.g., "John has twice as much as Mary") to mathematical expression through successive levels of discernment.
• Analyzing Reasoning in Math, Law, Logic: The model allows decomposing complex reasoning into perceptual and operational strata.
• Studying Logical Errors: One can pinpoint exactly at which level a confusion arises — for instance, mistaking a state for an operator, or a relation for a principle.

5. Cognition, Neuroscience, and Reasoning Psychology

• Modeling Mental Operations: The mathematical table aligns well with the actual sequence of mental operations, from quantity evaluation to systemic reasoning.
• Theory of Cognitive Development: Could serve as a map of the development of logical thinking in children (e.g., Piaget), and even in adults.
• Therapeutic or Neurodivergent Approaches: For particular cognitive profiles (autistic, dyscalculic, etc.), teaching could be adapted according to the levels where discernment fails or inverts.

6. Technical Applications

• In Systems Engineering: The ability to model systems as arrangements of values, relations, and principles allows for formalizing complex dynamic models.
• In Explainable AI (XAI): This framework can make algorithmic decisions more understandable by expressing them through the perceptual levels involved.
• In Game Theory or Optimization: It becomes possible to better distinguish strategies based on relations, transitions, or principles — and to model their evolution.

7. Metaphysics and Cognitive Cosmology

• Universal Model of Embodied Reasoning: In line with the metaphysics of THAT, this mathematical discernment expresses the way reality itself organizes through discernible interaction degrees.
• Link Between Mathematics and Reality: This model offers a bridge between the structure of the world (through complexity dimensions) and the structure of the reasoning that world enables.
• Embodied Formal Cosmology: If the world is perceived, structured, and modeled by an embodied consciousness, then mathematical discernment is the skeleton of the logical thought through which THAT understands itself.